Azimuthal Quantum Number: Definition, Importance, and Applications
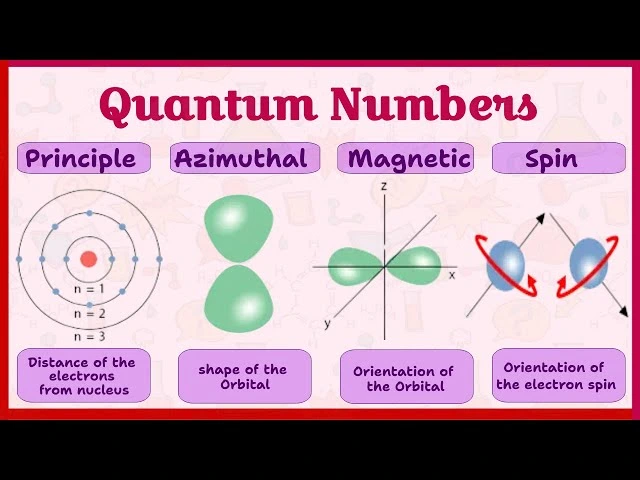
The azimuthal quantum number, also known as the angular momentum quantum number, is a key concept in quantum mechanics. It describes the shape and type of an atomic orbital, providing insights into the distribution of electrons around an atom's nucleus. Understanding the azimuthal quantum number is essential for comprehending atomic structure, electron configurations, and chemical bonding.
In this article, we’ll explore the definition, significance, possible values, and applications of the azimuthal quantum number in physics and chemistry.
What is the Azimuthal Quantum Number?
The azimuthal quantum number, denoted by l, is one of the four quantum numbers used to describe the quantum state of an electron in an atom. It determines the shape of the orbital and the subshell where the electron is located. The value of l also defines the orbital’s angular momentum.
Key Features:
- Shape of Orbitals:
- Determines the type of orbital: s, p, d, f, etc.
- Relation to Principal Quantum Number (n):
- The azimuthal quantum number depends on the principal quantum number and ranges from 0 to (n-1).
- Energy Levels:
- Electrons in subshells with higher l values generally have higher energy due to greater angular momentum.
Possible Values of Azimuthal Quantum Number
The azimuthal quantum number takes integral values from 0 to (n-1), where n is the principal quantum number. Each value of l corresponds to a specific subshell and orbital shape:
| Value of l | Subshell | Orbital Shape |
|---|---|---|
| 0 | s | Spherical |
| 1 | p | Dumbbell-shaped |
| 2 | d | Cloverleaf-shaped |
| 3 | f | Complex shapes |
For example:
- If :
Possible values of are 0 (s), 1 (p), and 2 (d).
Relationship Between Quantum Numbers
The azimuthal quantum number works in conjunction with other quantum numbers to describe an electron’s position and energy:
- Principal Quantum Number (n):
- Specifies the main energy level or shell.
- .
- The azimuthal quantum number depends on .
- Azimuthal Quantum Number (l):
- Defines the shape of orbitals within a shell.
- to .
- Magnetic Quantum Number (m):
- Specifies the orientation of orbitals in space.
- to .
- Spin Quantum Number (m):
- Indicates the spin of the electron.
- or .
Significance of Azimuthal Quantum Number
1. Determines Orbital Shape
- The azimuthal quantum number defines the geometry of electron clouds, influencing how atoms bond chemically.
2. Defines Subshells
- Helps classify subshells within an energy level, such as s, p, d, f, making it easier to understand electron configurations.
3. Angular Momentum
- Represents the angular momentum of an electron, which impacts the energy and stability of the atom.
4. Energy Splitting
- Differentiates subshells within the same energy level, explaining why p, d, and f orbitals have higher energies than s orbitals.
5. Chemical Bonding
- Influences how orbitals overlap during covalent bonding, affecting molecular shapes and properties.
Applications of Azimuthal Quantum Number
1. Understanding Electron Configurations
- The azimuthal quantum number is crucial for writing electron configurations.
- Example: For the element Oxygen (Z=8):
Electron configuration: .
Here, for s and for p orbitals.
2. Spectroscopy
- Explains energy transitions in atoms by detailing subshell splitting, which is crucial for understanding atomic spectra.
3. Chemical Reactivity
- Helps predict an atom’s bonding behavior by analyzing the shape and energy of orbitals.
4. Quantum Chemistry
- Used to solve the Schrödinger equation for multi-electron systems, providing insights into atomic and molecular structures.
5. Periodic Table Organization
- Justifies the arrangement of elements into blocks:
- s-block (),
- p-block (),
- d-block (),
- f-block ().
Differences Between Azimuthal and Principal Quantum Numbers
| Aspect | Principal Quantum Number (n) | Azimuthal Quantum Number (l) |
|---|---|---|
| Purpose | Defines the main energy level. | Defines the shape and type of orbital. |
| Values | Positive integers (1, 2, 3, …). | 0 to . |
| Energy Contribution | Major contributor to energy levels. | Minor contributor through angular momentum. |
| Example | : 3rd energy level. | : s, p, d subshells. |
Examples of Azimuthal Quantum Number
- For Hydrogen ():
- (s subshell).
- The single electron occupies a spherical s orbital.
- For Carbon ():
- : 2s subshell (spherical).
- : 2p subshell (dumbbell-shaped orbitals).
- For Transition Metals ():
- : d subshell (cloverleaf-shaped orbitals).
Advantages of Understanding Azimuthal Quantum Number
- Predicts Atomic Behavior:
- Helps understand how atoms interact and bond in molecules.
- Explains Spectral Lines:
- The splitting of spectral lines in atomic spectra can be attributed to differences in .
- Aids in Molecular Geometry:
- The shapes of orbitals impact molecular shapes and angles in compounds.
- Essential for Advanced Studies:
- Forms the basis for quantum chemistry, solid-state physics, and spectroscopy.
Conclusion
The azimuthal quantum number (l) is a cornerstone of quantum mechanics, providing valuable insights into atomic structure and electron behavior. By defining the shape and type of orbitals, it explains many fundamental phenomena in chemistry and physics, from electron configurations to chemical bonding and spectral analysis.