DDA Line Drawing Algorithm: Advantages, Applications & Implementation

By ParikshaPatr | November 29, 2024

The DDA Algorithm (Digital Differential Analyzer) is a foundational concept in computer graphics used for line generation. It is an efficient and straightforward technique for drawing lines on a screen by calculating intermediate points between two given endpoints. The DDA algorithm plays a vital role in raster graphics, where precision and computational efficiency are critical.

In this article, we’ll explore the DDA Algorithm, its working principles, advantages, applications, and a step-by-step implementation guide.

What is the DDA Algorithm?

The Digital Differential Analyzer (DDA) Algorithm is a rasterization algorithm that generates a straight line between two points in a pixel grid. It uses floating-point or integer arithmetic to calculate the incremental steps required to move along the line.

Key Features:

Incremental Approach: Calculates points incrementally, ensuring efficient computation.
Floating-Point or Integer Arithmetic: Can use floating-point for precision or integers for faster processing.
Linearity: Works on the principle of linear interpolation between two endpoints.

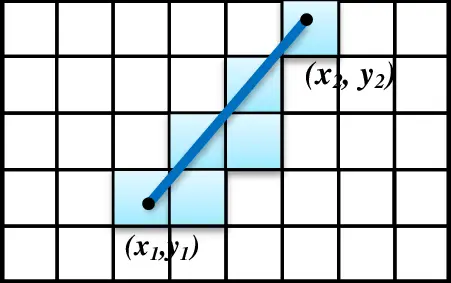
Steps in the DDA Algorithm

The DDA Algorithm involves calculating the slope of a line and incrementally plotting points based on the slope. Here’s a breakdown of the process:

Input the Endpoints:
- Accept the coordinates of the two endpoints: $(x_1, y_1)$ $($ $x$ $1$ $$ $,$ $y$ $1$ $$ $)$ and $(x_2, y_2)$ $($ $x$ $2$ $$ $,$ $y$ $2$ $$ $)$ .
Calculate the Slope ( $m$ m):
- Slope $m = (y_2 - y_1) / (x_2 - x_1)$ $m$ $=$ $($ $y$ $2$ $$ $-$ $y$ $1$ $$ $)$ $/$ $($ $x$ $2$ $$ $-$ $x$ $1$ $$ $)$ .
Determine Steps:
- Steps are based on the difference in x or y coordinates:
  $Steps$ $=$ $max$ $($ $∣$ $x$ $2$ $$ $-$ $x$ $1$ $$ $∣$ $,$ $∣$ $y$ $2$ $$ $-$ $y$ $1$ $$ $∣$ $)$
Calculate Increments:
- $x_{ ext{increment}} = Delta x / ext{Steps}$ $x$ $increment$ $$ $=$ $Δ$ $x$ $/$ $Steps$
- $y_{ ext{increment}} = Delta y / ext{Steps}$ $y$ $increment$ $$ $=$ $Δ$ $y$ $/$ $Steps$
Iterative Point Calculation:
- Start at $(x_1, y_1)$ $($ $x$ $1$ $$ $,$ $y$ $1$ $$ $)$ .
- Iteratively calculate intermediate points: $x = x + x_{ ext{increment}}, quad y = y + y_{ ext{increment}}$ $x$ $=$ $x$ $+$ $x$ $increment$ $$ $,$ $y$ $=$ $y$ $+$ $y$ $increment$ $$
- Round the values to the nearest pixel for plotting.
Plot the Line:
- Plot the calculated points on the pixel grid.

Pseudocode for DDA Algorithm

Here’s a simple pseudocode for the DDA Algorithm:

Input (x1, y1) and (x2, y2)
dx = x2 - x1
dy = y2 - y1

Steps = max(abs(dx), abs(dy))
x_increment = dx / Steps
y_increment = dy / Steps

x = x1
y = y1

for i = 0 to Steps:
    plot(round(x), round(y))
    x = x + x_increment
    y = y + y_increment
End

Example of DDA Algorithm

Given: Start Point $(2, 3)$ $($ $2$ $,$ $3$ $)$ , End Point $(8, 6)$ $($ $8$ $,$ $6$ $)$ .

Calculate dx and dy:
$dx = 8 - 2 = 6, quad dy = 6 - 3 = 3$ $dx$ $=$ $8$ $-$ $2$ $=$ $6$ $,$ $dy$ $=$ $6$ $-$ $3$ $=$ $3$ .
Determine Steps:
Steps = $max(|6|, |3|) = 6$ $max$ $($ $∣6∣$ $,$ $∣3∣$ $)$ $=$ $6$ .
Calculate Increments:
$x_{ ext{increment}} = dx / ext{Steps} = 6 / 6 = 1$ $x$ $increment$ $$ $=$ $dx$ $/$ $Steps$ $=$ $6/6$ $=$ $1$ ,
$y_{ ext{increment}} = dy / ext{Steps} = 3 / 6 = 0.5$ $y$ $increment$ $$ $=$ $dy$ $/$ $Steps$ $=$ $3/6$ $=$ $0.5$ .
Plot Points:
- Start: $(2, 3)$ $($ $2$ $,$ $3$ $)$ .
- Next points:
  $(3, 3.5) o (4, 4) o (5, 4.5) o (6, 5) o (7, 5.5) o (8, 6)$ $($ $3$ $,$ $3.5$ $)$ $\to$ $($ $4$ $,$ $4$ $)$ $\to$ $($ $5$ $,$ $4.5$ $)$ $\to$ $($ $6$ $,$ $5$ $)$ $\to$ $($ $7$ $,$ $5.5$ $)$ $\to$ $($ $8$ $,$ $6$ $)$ .

Advantages of the DDA Algorithm

Simplicity: Easy to implement and understand.
Precision: Provides better accuracy for line generation compared to older methods like Bresenham’s Algorithm.
Versatility: Can handle lines with arbitrary slopes.
Efficiency: Calculates points incrementally, reducing computational overhead.

Limitations of the DDA Algorithm

Floating-Point Computation: When using floating-point arithmetic, the algorithm can be slower on systems lacking hardware support.
Rounding Errors: Rounding floating-point values to integers may introduce slight inaccuracies in pixel plotting.
Integer Arithmetic Alternative: Integer-based DDA is faster but sacrifices some precision.

Applications of DDA Algorithm

Computer Graphics: Used in drawing straight lines, shapes, and curves in raster displays.
Game Development: Helps render 2D game environments by plotting pixel-perfect lines.
CAD Software: Creates precise lines and geometric shapes for design and modeling.
Image Processing: Facilitates drawing overlays or annotations on images.

DDA Algorithm vs. Bresenham’s Algorithm

Aspect	DDA Algorithm	Bresenham’s Algorithm
Calculation Type	Uses floating-point arithmetic.	Uses integer arithmetic.
Performance	Slower due to floating-point operations.	Faster due to integer operations.
Precision	More precise for arbitrary slopes.	May introduce rounding errors.
Implementation	Easier to understand and implement.	Slightly more complex.

Optimizing the DDA Algorithm

Use Integer Arithmetic: Convert floating-point operations to integers for better performance.
Hardware Acceleration: Modern GPUs can optimize DDA operations for faster rendering.
Error Correction: Implement error-handling mechanisms to reduce rounding inaccuracies.

Conclusion

The DDA Algorithm is a cornerstone in computer graphics, enabling precise and efficient line generation. Its simplicity and accuracy make it a preferred choice for many raster graphics applications, including game development, CAD software, and image processing.

Although modern alternatives like Bresenham’s Algorithm offer faster computation with integer arithmetic, DDA remains relevant for scenarios requiring floating-point precision and versatility.